Alors que je rédigeais le livret d’accompagnement pour une formation en astro que j’avais mené, je cherchais des illustrations pour mieux expliquer les différents principes de mécanique céleste. Mais je voulais que le style graphique de toutes les illustrations soit semblable. Récupérer des images toutes faites sur Wikipédia ne me convenait donc pas.

Comme je rédigeais le livret avec LaTeX, j’ai songé utiliser TikZ pour faire des dessins. J’ai trouvé quelques exemples (notamment sur l’excellent texample.net) d’illustrations du système solaire, mais je les trouvais trop austère. Je voulais quelque chose d’un peu plus cartoon, pour essayer de donner envie de lire.

J’ai alors décidé de faire toutes les figures moi-même avec TikZ. J’ai dessiné des petits schémas de planètes, de lunes et de soleils à placer n’importe où dans les figures. Une fois écrites les commandes pour dessiner les planètes, j’en ai fait un paquet que j’ai publié sur CTAN.

Voici les principes généraux et quelques exemples des possibilités offertes par cette bibliothèque, en combinaison avec d’autres fonctions de la bibliothèque TikZ.

Liste des exemples

• Équateur terrestre et inclinaison de la Terre
• Les phases de la Lune
• Une unité astronomique
• Les saisons et l’orbite de la Terre
• Les éclipses
• Inclinaison de l´orbite de la Lune
• Conjonctions, oppositions et quadratures
• Points de Lagrange
• Propriétés des planètes
• Coordonnées célestes

Les bases

Dans le préambule du document, on ajoute la ligne

\usepackage{planets}

Puis dans l’environnement tikzpicture, on dessine des planètes avec la commande \planet.

\documentclass[varwidth,margin=.3cm]{standalone} 
\usepackage{planets} 
\begin{document} 
\begin{tikzpicture}
\planet[]
\end{tikzpicture}
\end{document}

Définir l’allure d’une planète

On précise l’astre qu’on veut dessiner avec le mot-clé surface=. Les surfaces disponibles sont :

• sun, le Soleil
• mercury, Mercure
• venus, Vénus
• earth, la Terre
• moon, la Lune
• mars, Mars
• jupiter, Jupiter
• saturn, Saturne
• uranus, Uranus
• neputne, Neptune
• pluto, Pluton

Par exemple, vous pouvez utiliser \planet[surface=pluto] pour dessiner un de mes corps planétaires préférés.

Bien sûr, le Soleil, la Lune et Pluton ne sont pas des planètes, mais elles peuvent être dessinées avec les mêmes commandes que les autres.

On peut aussi ajouter une phase avec le mot-clé phase=. Les noms des phases sont :

• new
• first crescent
• first half
• waxing gibbous
• full
• waning gibbous
• last half
• last crescent
• top
• bottom

Par exemple, vous pouvez utiliser \planet[surface=moon, phase=first half]pour dessiner la Lune avec la moitié de sa face visible éclairée.

Si aucune phase n’est précisée dans les options de la commande \planet, alors aucune ombre n’est dessinée.

On peut aussi ajouter des anneaux autour de la planète en précisant leur diamètre avec le mot-clé ring=. On indique le diamètre des anneaux en unités de diamètres de la planète. Par exemple si on indique \planet[ring=2], alors les anneaux auront un diamètre égal à deux fois celui de la planète.

Saturne a des anneaux beaucoup plus larges que ceux des autres planètes gazeuses. Aussi, Saturne est dessinée par défaut avec ses anneaux. Pour dessiner des anneaux comme ceux de Saturne autour d’une autre planète, on utilise l’option rings.

La rotation d’une planète

Les planètes tournent sur elles-même autour d’un axe qui peut être incliné. L’axe de rotation d’une planète peut être ajouté au schéma avec l’option rotation. L’angle d’inclinaison en degrés de l’axe de rotation est indiqué avec le mot-clé tilt=.

Par exemple, vous pouvez utiliser \planet[surface=uranus, rotation, tilt=87] pour montrer que la planète Uranus « roule » sur le côté.

Le mot-clé tilt= modifie l’orientation de la surface de la planète, des anneaux (les anneaux des planètes connus sont dans le plan équatorial de leur planète hôte) et du segment qui indique la direction de l’axe de rotation de la planète.

Agencer plusieurs planètes dans une image

Pour avoir plusieurs planètes dans un même dessin, il faut pouvoir spécifier l’emplacement de chacune. Soit on indique le point où on veut placer le centre de la planète avec le mot-clé center=. Soit on peut préciser l’abscisse du centre avec centerx= et son ordonnée centery=. Si la position du centre de la planète n’est pas indiqué, alors elle est centrée en (0, 0).

Enfin, on peut modifier la taille des planètes avec le mot-clé scale=. Si aucune échelle n’est indiquée, le rayon par défaut est de 1.

---

Voilà les bases pour utiliser TikZ-planets. Maintenant, quelques exemples de son utilisation en pratique.

Équateur terrestre et inclinaison de la Terre

En astronomie, le pôle nord et le pôle sud sont les deux points de la surface terrestre par lesquels passent l’axe de rotation de la Terre. L'équateur est le cercle qui est à mi-distance entre les deux pôles.

L’axe qui relie le nord et le sud est incliné de 23.5° par rapport au plan qui contient l’orbite de la Terre.

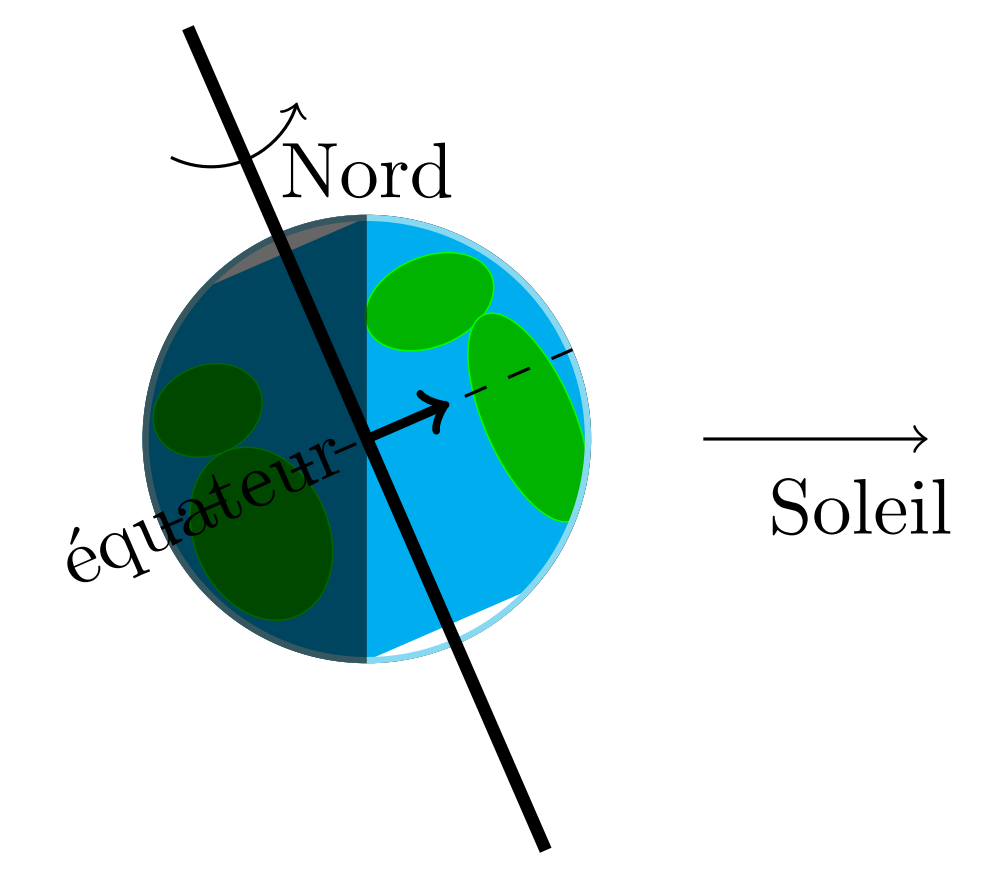
On trace la Terre (surface=earth) avec l’axe de rotation affiché (rotation). Son inclinaison est de 23.5° (tilt=23.5). Elle est éclairée par le Soleil sur sa moitié droite (phase=first half).

\begin{tikzpicture}
    \planet[surface=earth, rotation, tilt=23.5, phase=first half]
	
    \draw [->] (1.5, 0) -- (2.5, 0) ;
    \node (Sun) at (2.2, -.3) {Soleil};
	
    \node at (0, 1.2) {Nord};
    \node[anchor=east, rotate=23.5] at (0, 0) {équateur};
\end{tikzpicture}

Les phases de la Lune

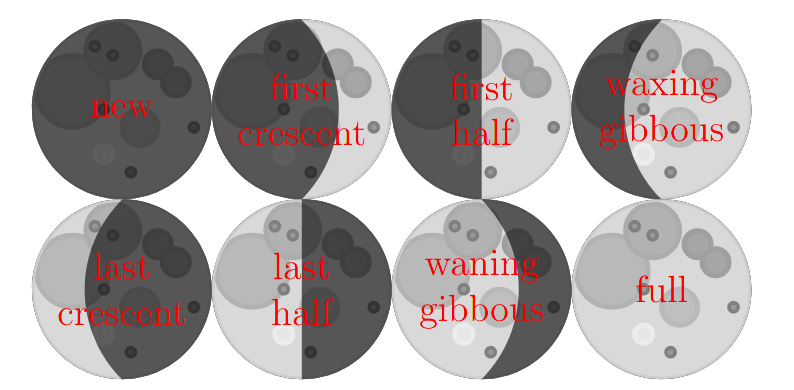
Pour illustrer les phases de la lune (et le nom des options disponibles pour le mot-clé phase=), on dessine huit lunes les unes à côté des autres. Leur position est spécifiée en créant un point avec la command \node et en utilisant ce point avec center=(nom du point). Au milieu de chaque planète, on écrit le nom de la phase correspondante.

\begin{tikzpicture}
    \node (new) at (0, 0) {};
    \planet[surface=moon, phase=new, center=(new)]
    \node[red] at (new) {new};

    \node (fc) at (2, 0) {};
    \planet[surface=moon, phase=first crescent, center=(fc)]
    \node[red, align=center] at (fc) {first \\ crescent};

    \node (fh) at (4, 0) {};
    \planet[surface=moon, phase=first half, center=(fh)]
    \node[red, align=center] at (fh) {first \\ half};

    \node (wxg) at (6, 0) {};
    \planet[surface=moon, phase=waxing gibbous, center=(wxg)]
    \node[red, align=center] at (wxg) {waxing \\ gibbous};

    \node (full) at (6, -2) {};
    \planet[surface=moon, phase=full, center=(full)]
    \node[red, align=center] at (full) {full};

    \node (wng) at (4, -2) {};
    \planet[surface=moon, phase=waning gibbous, center=(wng)]
    \node[red, align=center] at (wng) {waning \\ gibbous};

    \node (lh) at (2, -2) {};
    \planet[surface=moon, phase=last half, center=(lh)]
    \node[red, align=center] at (lh) {last \\ half};

    \node (lc) at (0, -2) {};
    \planet[surface=moon, phase=last crescent, center=(lc)]
    \node[red, align=center] at (lc) {last \\ crescent};
\end{tikzpicture}

Une unité astronomique

Une unité astronomique correspond à la distance Terre-Soleil, ou plus mathématiquement au demi-grand axe de l’orbite terrestre, soit 149 millions de kilomètres, ou encore 8 minutes-lumière.

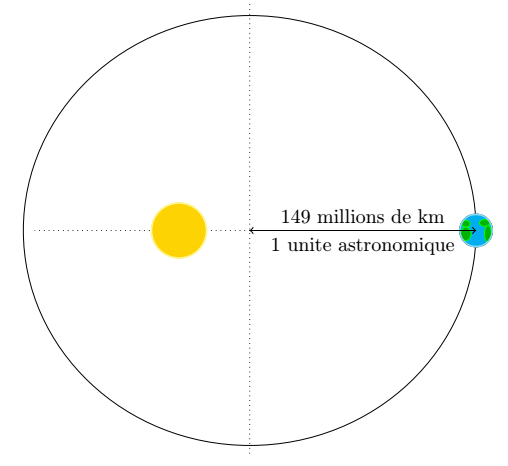
L’orbite de la Terre est une ellipse qu’on dessine avec une ellipse centrée en (0, 0) de demi-grand axe \a et de demi-petit axe \b. Le Soleil est situé à l’un des foyers de cette ellipse, en (0, \f). On calcule dans LaTeX la position du foyer à partir du demi-grand axe et du demi-petit axe de l’ellipse.

\begin{tikzpicture}
\def\a{4} % demi-grand axe
    \def\b{3.8} % demi-petit axe
    \def\f{{-sqrt(\a*\a-\b*\b)}} % position du foyer de l'ellipse

    % Orbite de la Terre
    \draw (0,0) ellipse ({\a} and {\b});

    % Axes de l'ellipse
    \draw[dotted] (0, \a) -- (0, -\a);
    \draw[dotted] (\b, 0) -- (-\b, 0);

    % Soleil
    \planet[surface=sun, centerx=\f, scale=.5]

    % Terre
    \planet[surface=earth, centerx=\a, scale=.3]

    % Unité astronomique
    \draw[<->] ({\a}, 0) -- node[below] {1 unite astronomique} node[above] {149 millions de km} (0, 0) ;
\end{tikzpicture}

Les saisons et l’orbite de la Terre

Les saisons sont causées par l’inclinaison à 23.5 degrés de l’axe de rotation de la Terre et par le mouvement de la Terre autour du Soleil. Pour cette raison, lorsque c’est l'été dans l’hémisphère nord, c’est l’hiver dans l’hémisphère sud, et vice versa.

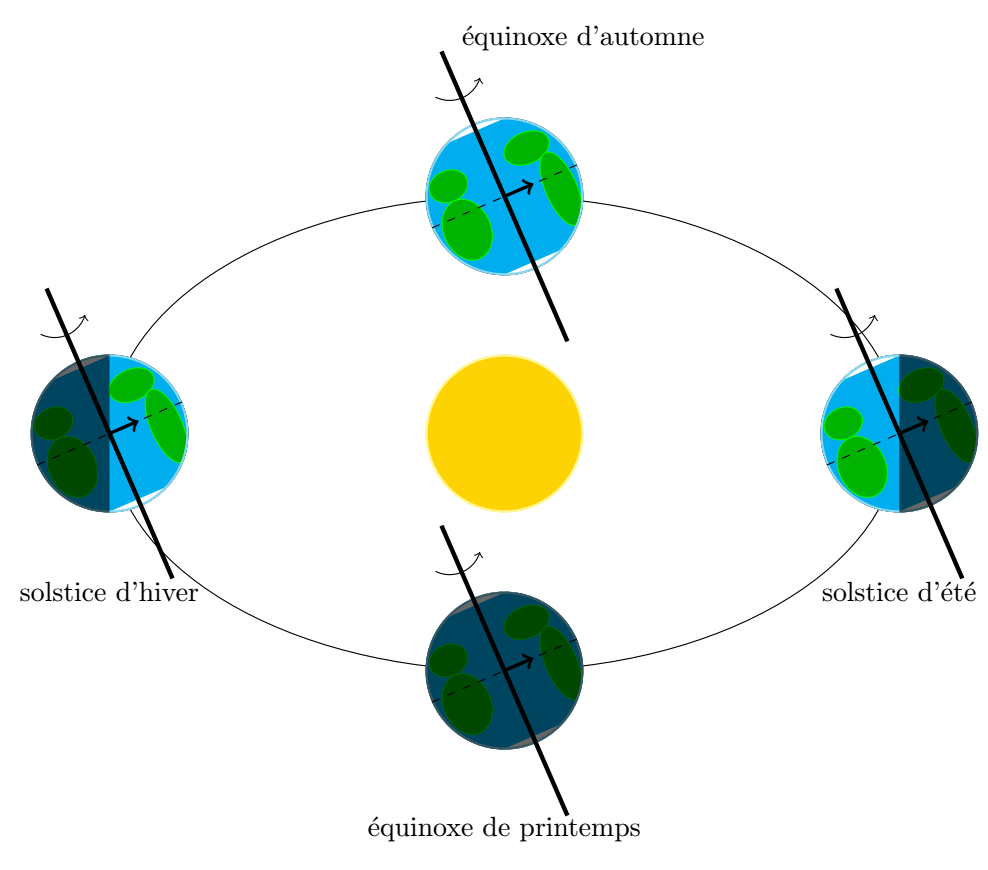
Ici, on dessine le Soleil au centre, avec la Terre dans quatre positions différentes et avec quatre phases différentes. L´axe de rotation de la Terre est de constant au cours de la rotation autour du Soleil (tilt=23.5).

\begin{tikzpicture}
    \planet[surface=sun]
    \draw (0, 0) circle (5 and 3);

    \planet[surface=earth, phase=first half, rotation, tilt=23.5, centerx=-5]
    \node at (-5, -2) {solstice dhiver};

    \planet[surface=earth, phase=last half, rotation, tilt=23.5, centerx=5]
    \node at (5, -2) {solstice dété};

    \planet[surface=earth, phase=new, rotation, tilt=23.5, centery=-3]
    \node at (0, -5) {équinoxe de printemps};

    \planet[surface=earth, phase=full, rotation, tilt=23.5, centery=3]
    \node at (1, 5) {équinoxe dautomne};
\end{tikzpicture}

Les éclipses

Lorsque la Lune passe directement entre la Terre et le Soleil, il se produit une éclipse solaire.

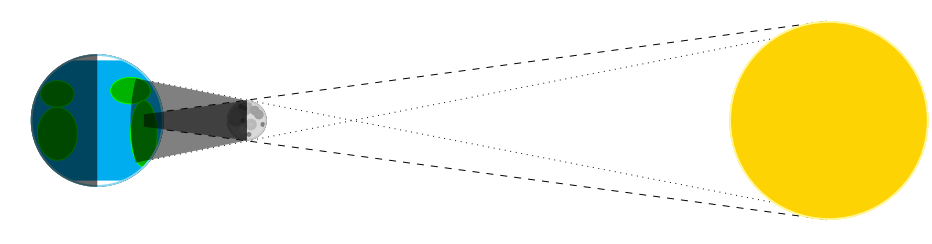
Là, c’est un peu plus technique, il a fallu que je fasse quelques calculs sur un coin de feuille pour que tous les traits se croisent au bon endroit.

    \draw[dashed] (-3, 0) -- (8, 1.5);
    \draw[dashed] (-3, 0) -- (8, -1.5);

    \draw[dotted] (-3, -0.76) -- (8, 1.5);
    \draw[dotted] (-3, 0.76) -- (8, -1.5);

    % Les trois astres
    \planet[surface=moon, scale=.3, centerx=-.75]
    \planet[surface=sun, centerx=8, scale=1.5]
    \planet[surface=earth, centerx = -3, phase=first half]

    % Ombre
    \begin{scope} 
        \clip[overlay] (-.1, 0) circle (2.2);
        \fill[opacity=.5] (-.75, .3) -- (-3, 0) -- (-.75, -.3) -- cycle;
    \end{scope}

    % Pénombre
    \begin{scope}
        \clip[overlay] (0, 0) circle (2.5);
        \fill[opacity=.5] (-.75, .3) -- (-3, .75) -- (-3, -.75) -- (-.75, -.3) -- cycle;
    \end{scope}
\end{tikzpicture}

Lorsque la Lune passe dans l’ombre de la Terre, il se produit une éclipse lunaire.

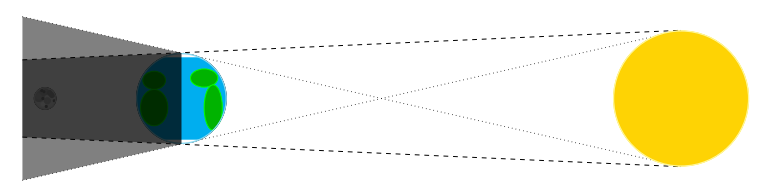
\begin{tikzpicture}
    \draw[dashed] (-3.5, .85) -- (11, 1.5);
    \draw[dashed] (-3.5, -.85) -- (11, -1.5);

    \draw[dotted] (-3.5, -1.8) -- (11, 1.5);
    \draw[dotted] (-3.5, 1.8) -- (11, -1.5);

    \planet[surface=moon, scale=.25, centerx=-3]
    \planet[surface=sun, centerx=11, scale=1.5]
    \planet[surface=earth, centerx = 0]

    \fill[opacity=.5, black] (0, 1) -- (-3.5, .85) -- (-3.5, -.85) -- (0, -1) -- cycle;
    \fill[opacity=.5, black] (0, 1) -- (-3.5, 1.8) -- (-3.5, -1.8) -- (0, -1) -- cycle;
\end{tikzpicture}

Inclinaison de l´orbite de la Lune

S’il n’y a pas une éclipse chaque mois, c’est parce que l’orbite de la Lune autour de la Terre est inclinée par rapport à l’orbite de la Terre autour du Soleil.

Là, je triche un peu. L’inclinaison de l’orbite lunaire est de 5°, mais pour éviter que le schéma soit illisible (ou beaucoup trop grand), je représente l’orbite avec une inclinaison de 10°.

\begin{tikzpicture}
    \draw[dashed, color=cyan!50!black] (-10, 0) --  (2, 0);
    \node[above right, color=cyan!50!black] at (-8, 0) {écliptique};

    \draw[dotted] (190:2.5) -- (10:2.5);

    \planet[surface=sun, centerx=-10]

    \planet[surface=earth, scale=.2]

    \planet[surface=moon, scale=.1, centerx=-2, centery=-.4]
    \planet[surface=moon, scale=.1, centerx=2, centery=.4]

    \draw [<->] (180:2.2) to [bend right=30]  node [left] {5$^\circ$} (190:2.2);
\end{tikzpicture}

Conjonctions, oppositions et quadratures

Pour les planètes supérieures, on appelle conjonction le moment où la planète est derrière le Soleil, opposition le moment où la planète est la plus proche de nous (à l´opposé dans le ciel par rapport au Soleil) et quadrature le moment où le Soleil, la Terre et la planète supérieure forment un angle droit.

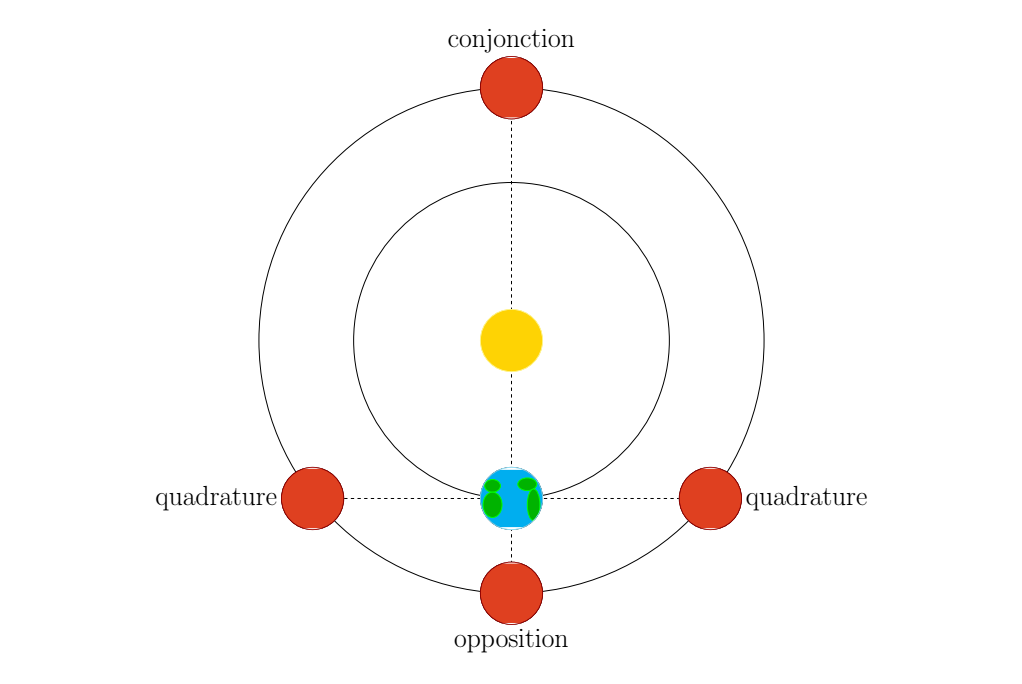
\begin{tikzpicture}
    \draw[dashed] (-5.3, 0) -- (5.3, 0);
    \draw[dashed] (0, 13) -- (0, -3);
    
    \draw (0, 5) circle (5);
    \planet[surface=earth]
    \planet[surface=sun, centery=5]
    
    \draw (0, 5) circle (8);    
    \planet[surface=mars, centery=-3]
    \node[below] at (0, -4) {\Huge opposition};
    
    \planet[surface=mars, centery=13]
    \node[above] at (0, 14) {\Huge conjonction};
    
    \planet[surface=mars, centerx=6.3]
    \node[right] at (7.3, 0) {\Huge quadrature};
    
    \planet[surface=mars, centerx=-6.3]
    \node[left] at (-7.3, 0) {\Huge quadrature};
\end{tikzpicture}

Points de Lagrange

Dans le problème à trois corps, il existe certaines configurations stables, appelées points de Lagrange.

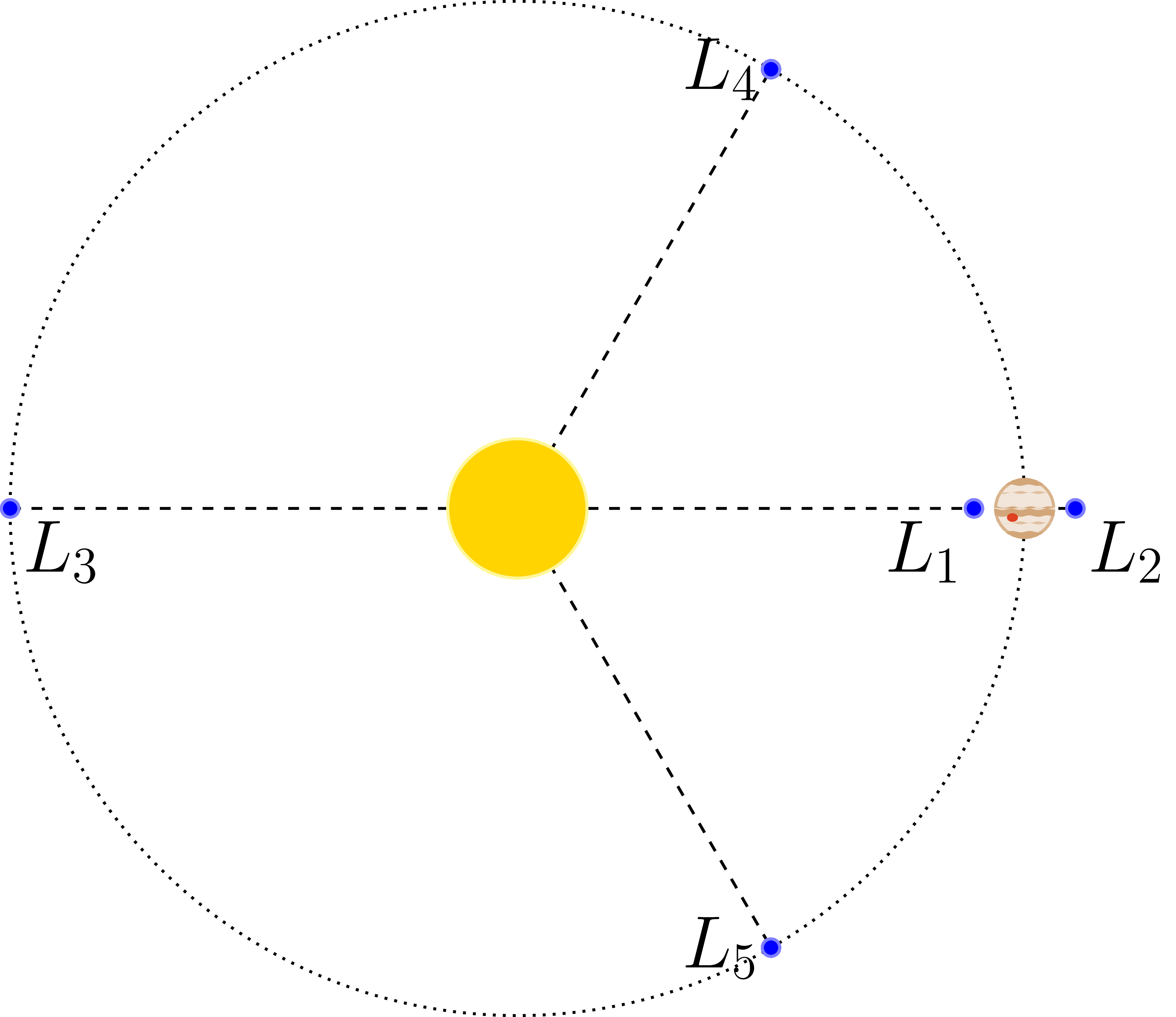
\begin{tikzpicture}
\draw [thick, dashed] (-5, 0) -- (5.5, 0);
\draw [thick, dashed] (0, 0) -- (60:5);
\draw [thick, dashed] (0, 0) -- (-60:5);

\draw [thick, dotted] (0, 0) circle (5);
\planet[surface=sun, scale=.7]
\planet[surface=jupiter, center={(5, 0)}, scale=.3]

\planet[color=blue, scale=.1, center={(60:5)}]
\node [left] at (60:5) {\huge $L_4$};

\planet[color=blue, scale=.1, center={(-60:5)}]
\node [left] at (-60:5) {\huge $L_5$};

\planet[color=blue, scale=.1, center={(4.5, 0)}]
\node [below left] at (4.5, 0) {\huge $L_1$};

\planet[color=blue, scale=.1, center={(5.5, 0)}]
\node [below right] at (5.5, 0) {\huge $L_2$};

\planet[color=blue, scale=.1, center={(-5, 0)}]
\node [below right] at (-5, 0) {\huge $L_3$};
\end{tikzpicture}

Propriétés des planètes

On peut classifier les planètes en fonction de leur masse, de leur diamètre et du demi-grand axe de leur orbite.

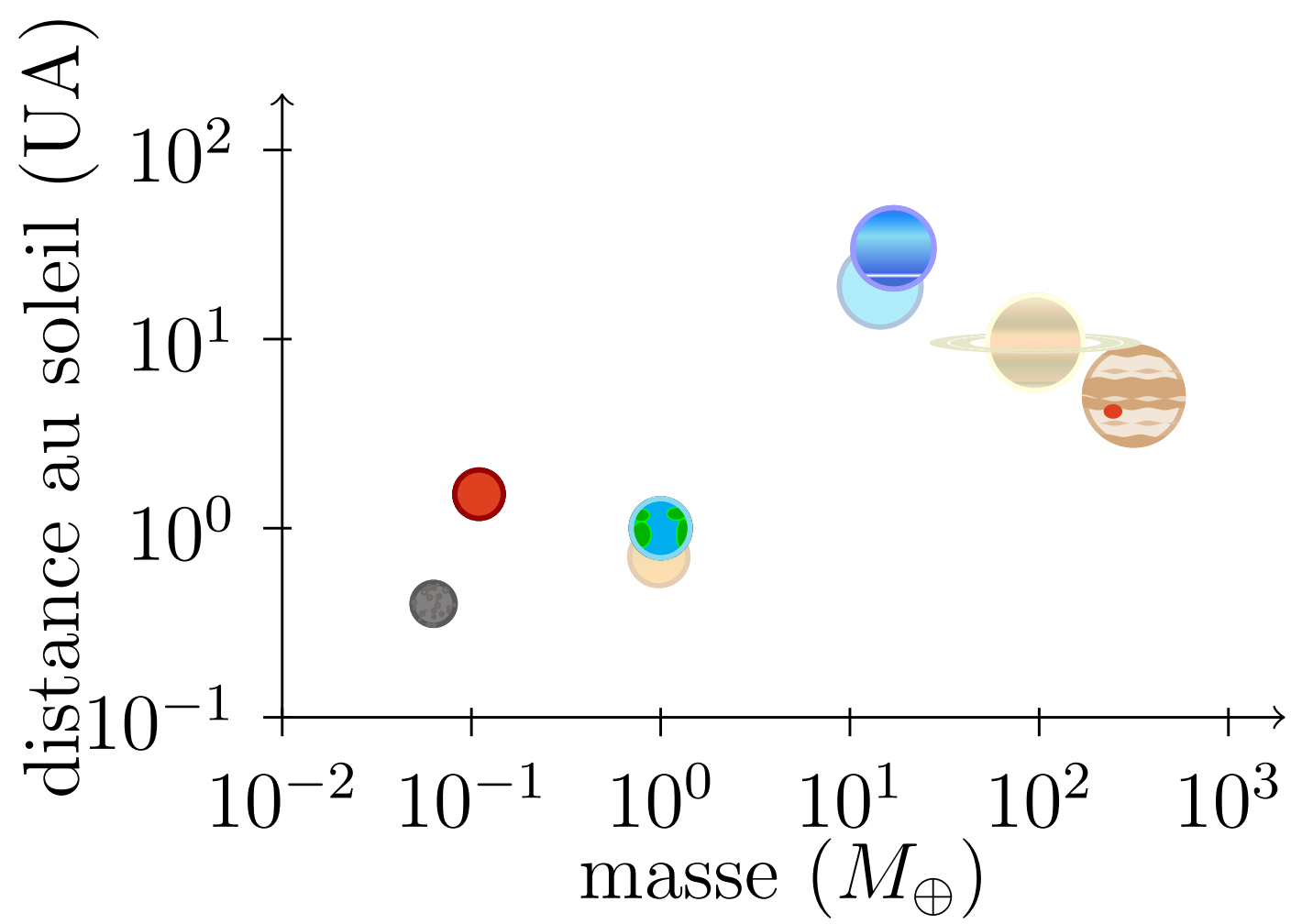
\begin{tikzpicture}

% On défini d'abord quelques macros pour faciliter la création des axes du graphique
\pgfmathsetmacro{\xorigin}{-2}
\pgfmathsetmacro{\yorigin}{-1}
\pgfmathsetmacro{\xend}{3.3}
\pgfmathsetmacro{\yend}{2.3}
\pgfmathsetmacro{\xtwo}{-1}
\pgfmathsetmacro{\ytwo}{0}
\pgfmathsetmacro{\ticksize}{0.1}

\coordinate (origin) at (\xorigin, \yorigin);
\coordinate (absend) at (\xend, \yorigin);
\coordinate (ordend) at (\xorigin, \yend);

% Puis on trace les axes...
\draw [->] (origin) -- coordinate (xmid) (absend);
\draw [->] (origin) -- coordinate (ymid) (ordend);

% ... avec leurs graduations
\foreach \x in {\xorigin, \xtwo,...,\xend}
	\draw (\x, \yorigin + 0.5*\ticksize) -- (\x, \yorigin - \ticksize)
	node[anchor=north] {$10^{\pgfmathprintnumber\x}$};
\foreach \y in {\yorigin, \ytwo,...,\yend}
	\draw (\xorigin + 0.5*\ticksize, \y) -- (\xorigin - \ticksize, \y)
	node [anchor=east]{$10^{\pgfmathprintnumber\y}$};

% On place la légende des axes
\node[below = 1.2em] at (xmid) {masse ($M_\oplus$)}; %xaxis
\node[rotate = 90, above = 2em] at (ymid) {distance au soleil (UA)}; %yaxis

% Enfin, on place les planètes au bon endroit, avec le diamètre qui est fonction du diamètre réel
\planet[surface=mercury, center={(-1.2, -0.4)}, scale=0.128]
\planet[surface=venus, center={(-.01, -.15)}, scale=0.168]
\planet[surface=earth, center={(0, 0)}, scale=0.170]
\planet[surface=mars, center={(-0.96, 0.18)}, scale=0.142]
\planet[surface=jupiter, center={(2.5, 0.7)}, scale=0.275]
\planet[surface=saturn, center={(1.98, 0.98)}, scale=0.267]
\planet[surface=uranus, center={(1.16, 1.28)}, scale=0.230]
\planet[surface=neptune, center={(1.23, 1.48)}, scale=0.229]

\end{tikzpicture}

Coordonnées célestes

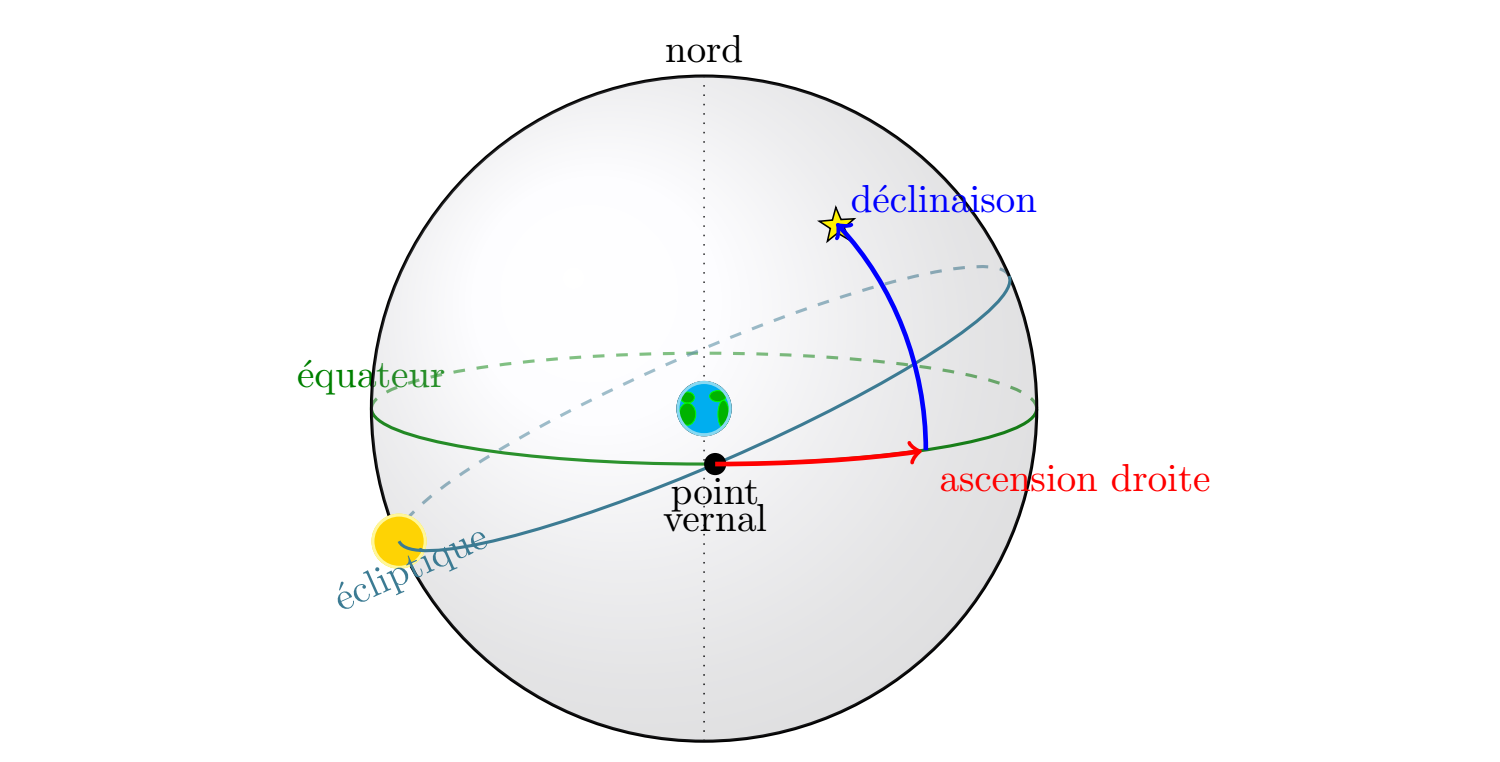
Enfin, voilà le code qui a servi à faire l’image au tout début de cet article.

Afin de dessiner l'étoile, il faut importer une bibliothèque TikZ supplémentaire en ajoutant la commande \usetikzlibrary{shapes} dans l’en-tête.

\begin{tikzpicture}%
\node (dec) at (1.2, 1.65) {};
\node (ad) at (2, -.375) {};

% Axe nord-sud
\draw[dotted] (0, -3) -- (0, 3);
\node[above] at (0, 3) {nord};

% Équateur
\draw[thick, color=green!50!black] (-3,0) arc (180:360:3 and .5);
\draw[thick, dashed, opacity=.6, color=green!50!black] (-3,0) arc (180:0:3 and .5);
\node[color=green!50!black, above] at (-3, 0) {équateur};

% Écliptique (arrière)
\draw[thick, dashed, rotate=23.5, color=cyan!50!black, opacity=.6] (-3,0) arc (180:0:3 and .5);
% Celestial sphere
\draw[thick] (0,0) circle (3);
\shade[ball color=blue!5!white,opacity=0.20] (0,0) circle (3);

% Terre
\planet[surface=earth, scale=.25]
% Soleil
\planet[surface=sun, scale=.25, centerx = -2.751, centery = -1.196]

% Ecliptique (avant)
\draw[thick, rotate=23.5, color=cyan!50!black] (-3,0) arc (180:360:3 and .5);
\node[color=cyan!50!black, rotate=24, below] at (203.5:3) {écliptique};

% Point vernal
\node (gamma) at (0.1,-.5)  {};
\node[below, align=center] at (gamma) {point \\[-.5em] vernal};
\fill(gamma) circle (.1);

% Étoile
\node[star,star points=5, draw, fill=yellow, star point ratio=0.4, rotate=40] (star) at (dec) {};

% Ascension droite
\draw[red, very thick, ->] (gamma) arc (-90:-50:2.9 and .5);
\node[below right, red] at (ad) {ascension droite};

% Déclinaison
\draw[blue, very thick, ->] ++(ad) arc (0:43:3);
\node [blue, above right] at (dec) {déclinaison};
\end{tikzpicture}

Conclusion

Voilà quelques exemples de ce qu’il est possible de faire avec TikZ-planets. J’espère que cet article vous donnera envie d’utiliser cette bibliothèque pour faire vos propres diagrammes.